En este artículo se describe la propagación de las señales acústicas en entornos subacuáticos, en los cuales las mismas cobran una importancia análoga a la radiofrecuencia en aire. En esta primera parte  se abordará una breve revisión histórica, los parámetros fundamentales de los que depende la propagación acústica en el agua y en la segunda parte se verán diversos modelos existentes que estudian dicha propagación. En una tercera parte se verán otros mecanismos que afectan a la propagación de las ondas acústicas en el agua, y se mostrarán diversas simulaciones de la propagación acústica bajo diferentes condiciones.

En las últimas décadas ha cobrado especial importancia el empleo de las señales acústicas en medios subacuáticos, debido a la necesidad de monitorizar diversos sensores medioambientales, controlar robots sumergidos con cierto grado de libertad, el uso del sónar, etc. Ya que la utilización de cables no es económica o práctica de forma general en este medio, las comunicaciones inalámbricas, y más concretamente las acústicas, ha sido la solución más empleada para solventar esta restricción.

El medio subacuático presenta unas propiedades que favorecen especialmente el empleo de ondas acústicas en lugar de las ondas electromagnéticas. Las ondas electromagnéticas experimentan una atenuación muy elevada en el agua, del orden del dB·m-1 para una frecuencia de 30 kHz, mientras que una onda acústica a esa misma frecuencia presenta una atenuación del orden del dB·km-1. Por otra parte, las frecuencias ópticas se encuentran tan afectadas por el scattering y la dispersión que el medio se vuelve opaco más allá de distancias superiores a 200 metros para estas frecuencias [1]. Debido a estos problemas, el uso de las ondas electromagnéticas en el agua se encuentra muy restringido.

En general, el medio subacuático presenta unos efectos muy parecidos al atmosférico: atenuación y absorción de la señal por el medio, la presencia de ruido, la variabilidad espacial y temporal que presenta, efecto Doppler, capas de burbujas, corrientes internas y muy especialmente el multicamino. Estos mecanismos provocan que la señal pueda llegar al receptor bastante degradada.

Breve revisión histórica
De forma general, se considera que el precursor de la investigación de la propagación acústica en el agua es Leonardo da Vinci, que ya a finales del siglo XV sentó las bases para un rudimentario sónar pasivo (basado en la recepción de una señal generada por el objetivo, no un eco). La idea de Leonardo da Vinci, era que si una persona viaja en un barco y éste se para en mitad del mar, colocando un extremo de un tubo lo suficientemente largo en el agua y acercando el oído al otro extremo, se podrían escuchar barcos distantes [2].
Años más tarde, en 1827, se midió la velocidad del sonido en el agua mediante un experimento realizado en el lago Geneva por el físico Daniel Colladon y el matemático Charles François Sturm. Para ello se generaron dos señales simultáneas: un destello luminoso y el sonido de una campana sumergida, y se midió el intervalo de tiempo entre la observación de ambas recepciones. Este experimento permitió estimar la velocidad del sonido en el agua en 1435 m·s-1 para una temperatura de 8ºC [3].

Dentro del siglo XIX habría que destacar también la contribución que tuvieron los avances en otros campos, como el descubrimiento del efecto de magnetostricción en 1840 por James Joule, y del efecto piezoeléctrico en 1880 por Pierre y Jacques Curie [2]. Estos efectos permitirían generar ondas acústicas de un contenido espectral específico.
En el siglo XX se produjeron varios avances relacionados con las Guerras Mundiales. En la Primera Guerra Mundial se utilizaba todavía un sónar basado en la idea de Leonardo da Vinci, pero modificado con un segundo tubo para discriminar mejor la dirección de llegada de las ondas acústicas. Durante esta guerra se comenzaron a desarrollar los primeros experimentos encaminados a un sónar activo, es decir, basado en el reconocimiento del eco producido por la señal acústica en un objeto. Se llegaron a detectar ecos de submarinos a distancias de un kilómetro y medio [2].
En 1919 se publica el que se considera el primer artículo de investigación sobre acústica subacuática. El autor fue H. Lichte, y estudiaba la influencia de capas horizontales de distinta temperatura en la propagación de las ondas acústicas [2].

En 1945 se desarrolló uno de los primeros sistemas de comunicación subacuática, que se empleaba en submarinos y tenía un alcance de varios kilómetros de distancia. Empleaba una modulación en banda lateral única y un rango de frecuencias entre 8 y 11 kHz [4].
A partir de este punto, y más tarde con el desarrollo de la tecnología VLSI (Very-Large-Scale Integration) en circuitos integrados y la aparición de los DSP (Digital Signal Processor), se comienza a experimentar con distintas modulaciones, ecualizaciones y proceso de corrección de errores que fueron mejorando progresivamente el rendimiento de estos sistemas.
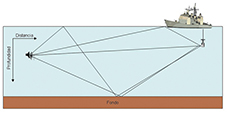
A principios de los años 70, C.S. Miller y C.E. Bohman emplearon el salto de frecuencia como medida para disminuir los efectos provocados por el multicamino, utilizando además una modulación en fase combinada con una modulación en frecuencia [5]. De entre todos los efectos presentes, se identificaba al multicamino como la principal dificultad a la hora de establecer una comunicación. Este efecto es más notable en transmisiones a lo largo del eje de distancias, puesto que aparecen más rebotes que en una transmisión en el eje de profundidades. La Figura 1 representa una situación donde se realiza una propagación en el eje de distancias, y en la que aparecen distintos caminos que puede seguir la señal hasta el receptor (camino directo, un rebote en el fondo, etc.), formando así el multicamino.

Las velocidades de transmisión alcanzadas durante la década de 1980 rondaban el kilobit por segundo, en experimentos realizados mediante modulación en frecuencia o modulación en fase, como los recogidos en [6] o [7].
En la década de los 90 se comienza a generalizar el uso de la modulación en fase en detrimento de la modulación en frecuencia. En 1992, empleando esta modulación, se alcanzan velocidades de 16 kbps en una transmisión a lo largo del eje de profundidades [8]. En 1994 R. Galvin y R.F.W. Coates desarrollan un sistema que alcanza velocidades de 10 kbps para una transmisión en el eje de distancias, donde el emisor y el receptor están separados 2 km [9]; en el caso de situar el receptor a 900 m del emisor, la velocidad de transmisión era de 20 kbps. Y un par de años más tarde, en 1996, el Instituto Oceanográfico de Woods Hole desarrolla un sistema que alcanza cotas de 40 kbps para una distancia de 2 km [10].

A partir de este punto las distintas contribuciones no consisten tanto en aumentar la velocidad, sino en emplear otras configuraciones. Por nombrar algunos ejemplos, en 1999 aparece un sistema desarrollado por E.M. Sozer et al. basado en la técnica de espectro ensanchado por secuencia directa (Direct Sequence Spread Spectrum, DSSS) [11]. En 2004 D. Kilfoyle utiliza la técnica de modulación espacial (spatial modulation) y un receptor multiusuario que aprovecha la variabilidad espacial del multicamino, consiguiendo incrementar la capacidad del canal entre dos y tres veces [12]. Comienzan a aparecer cada vez más estudios para implementar redes de sensores subacuáticos, como el publicado por Akyildiz et al. en 2005 [13], y aparecen otras posibilidades para la modulación, como OFDM (Orthogonal Frequency Division Multiplexing) [14]. En 2007, S. Roy et al. proponen la codificación espacio-temporal (space-time coding) junto a una ecualización iterativa, obteniéndose velocidades de 48 kbps [15].

Parámetros fundamentales de la propagación acústica subacuática
La velocidad del sonido y las pérdidas de transmisión son los dos parámetros fundamentales en lo que respecta a la propagación de una onda acústica en un medio subacuático. La variación de la velocidad del sonido con la profundidad determinará lo que se conoce como “perfil de la velocidad del sonido”, que según su forma favorecerá la propagación de la onda acústica de una manera particular. Las pérdidas de transmisión vienen dadas por los distintos factores que atenúan la onda acústica en su recorrido por el medio subacuático.

Velocidad del sonido
De forma rigurosa, la velocidad del sonido se obtiene a partir de la ecuación de ondas lineal [1], y su valor es el que aparece en la ecuación (1):

Donde c es la velocidad del sonido en m·s-1, g  es el índice adiabático, BT es el módulo de compresibilidad isotérmico y r0 la densidad de equilibrio. A su vez, estas tres magnitudes son función de la temperatura y de la presión del agua.
Obtener una expresión donde queden reflejadas de forma clara estas variaciones es complicado, de forma que lo habitual es expresar la velocidad del sonido mediante expresiones semi-empíricas, que dependerán entonces de las medidas realizadas, existiendo un amplio número de ecuaciones. Por ejemplo, una ecuación para el agua destilada es la expresada en la ecuación (2) [1]:

Donde c es la velocidad del sonido en m·s-1, t = T/100, donde T es la temperatura en grados Celsius, y   es la presión de gauge expresada en bares, donde un valor igual a 0 bar indica una presión de equilibrio de 1.01325 bar (1 atm). Esta ecuación es válida para temperaturas entre 0ºC y 100ºC, y presiones de gauge entre 0 y 200 bar.
El medio subacuático más utilizado en la propagación de las ondas acústicas es el océano (o los distintos mares), y por ello se hablará por defecto de fondo marino o fondo oceánico, así como de superficie del mar, aunque los resultados se pueden extrapolar a otros medios subacuáticos. El agua de mar es distinta de la destilada en lo que respecta a las variables que influyen en la velocidad del sonido, introduciendo otro factor más: la salinidad. A lo largo de las últimas décadas, han surgido diferentes ecuaciones para expresar la velocidad del sonido en medios marinos, donde las más importantes son las ecuaciones de Del Grosso y de Chen y Millero. Esta última ecuación fue reconocida por la UNESCO como el algoritmo estándar para calcular la velocidad del sonido para medios subacuáticos [16].
La ecuación de Del Grosso data originalmente de 1974 y se expresa, en su forma corregida posteriormente, según la ecuación (3). Los coeficientes DCi engloban a su vez a otros (un total de 18) que pueden ser función de la temperatura (T), presión (P) y salinidad (S) [16]:

Esta ecuación es válida para temperaturas entre 0ºC y 30ºC, salinidades entre 30‰ y 40‰, y presiones entre 0 kg·cm2 y 100 kg·cm².
La ecuación de Chen y Millero data por su parte de 1977, y en su forma corregida posteriormente se expresa según la ecuación (4), donde al igual que en el caso anterior, los coeficientes que aparecen engloban a su vez a otros (un total de 42), que pueden depender de la temperatura (T), presión (P) y salinidad (S) [16]:

Esta ecuación es válida para temperaturas entre 0ºC y 40ºC, salinidades entre 0‰ y 40‰ y una presión entre 0 y 1000 bar.
No existe una diferencia apreciable entre los resultados obtenidos por ambas ecuaciones en los rangos de validez donde se solapan. Por ejemplo, se puede estudiar cómo varían las velocidades obtenidas por ambas expresiones cuando se varía la temperatura. Este resultado se muestra en la Figura 2, donde se aprecia que el valor obtenido es prácticamente idéntico. Se obtiene un resultado análogo si se consideran variaciones con la presión o la salinidad.
Una vez que se obtiene un valor para la velocidad del sonido en función de la temperatura, la presión y la salinidad, se puede estudiar cómo varía esta velocidad respecto a la profundidad, para obtener así el perfil de la velocidad del sonido. Para ello, hay que conocer cómo varían la temperatura, la salinidad y la presión respecto a la profundidad.

En general, la variación de la salinidad con la profundidad es despreciable, salvo en regiones específicas como zonas polares o estuarios. La velocidad del sonido varía 1 m·s-1 por cada parte por mil que varía la salinidad, y ésta no suele variar más de 3‰ en una región dada, y 10‰ entre distintos océanos y zonas del mundo. Por otra parte, la velocidad del sonido varía 5 m·s-1 por cada grado Celsius, y 1.6·10-6 m·s-1 por cada Pascal, donde a su vez, tanto la temperatura como la presión dependen de la profundidad [3]. La variación de la velocidad del sonido con la presión puede parecer despreciable, pero ésta aumenta a un ritmo de 1 atm por cada 10 m de profundidad. A 1 km la presión sería aproximadamente de 100 atm, o lo que es lo mismo, 10132500 Pa, de manera que la velocidad del sonido varía aproximadamente unos 16 m·s-1 en el primer kilómetro [1]; este efecto es notable en los océanos, donde la profundidad puede alcanzar algunos kilómetros.
Teniendo en cuenta todos estos efectos, se obtiene el perfil de la velocidad del sonido, que para latitudes medias tiene la forma típica dada en la Figura 3. A profundidades elevadas, la temperatura se mantiene prácticamente constante, de manera que como la salinidad apenas varía con la profundidad, los cambios en la velocidad del sonido vienen dados por la variación de la presión con la profundidad. Ésta disminuye a medida que la superficie está más cerca, por lo que la velocidad del sonido disminuye también. En la Figura 3, este comportamiento se da hasta una profundidad en torno al kilómetro, donde se produce un mínimo en el valor de la velocidad del sonido. La región que ocupa desde el fondo oceánico hasta el mínimo, se denomina capa isotérmica profunda. 

Para valores menores de esta profundidad, comienza a notarse el efecto de la temperatura, aumentando a medida que se aproxima la superficie del mar, siendo éste efecto más importante que el de la variación de la presión con la profundidad. Esta zona, que se extiende desde los 1000 m hasta una profundidad de 200 m aproximadamente, se denomina termoclina principal, y en ella el efecto de las estaciones es despreciable. Entre los 200 m y los 100 m se tiene una región donde los efectos estacionales sí son apreciables, de manera que la forma del perfil en esta región varía en función de la estación. Esta región se denomina termoclina estacional. Entre los 100 m y la superficie aparece una zona expuesta a los cambios atmosféricos, ya sea el viento o cambios bruscos de temperatura y movimiento de masas de agua. Este movimiento de masas de agua produce una mezcla que hace que esta región pueda considerase como isoterma, a pesar de los cambios bruscos de temperatura que pueda sufrir. Por ello se denomina capa superficial o de mezcla.

El perfil aquí descrito es válido para latitudes medias, pero de forma general varía con la latitud y las condiciones particulares del lugar. Por ejemplo, en una región polar no se produce el aumento de temperatura a medida que se aproxima la superficie, por lo que la capa isotérmica profunda se extiende hasta la superficie, y en otras zonas, la profundidad del mínimo de la velocidad del sonido puede ser distinta al kilómetro.
Una vez que se conoce la forma del perfil de la velocidad del sonido, se puede determinar cómo se va a propagar la señal acústica por el medio subacuático. Debido al principio de Huygens y dada la forma del perfil de la velocidad del sonido, se forman zonas donde las ondas que surgen de los frentes de onda se propagarán a velocidades distintas en función de la profundidad a la que se encuentren dichos frentes. El efecto neto es la curvatura de la onda acústica hacia la región donde la velocidad del sonido es menor. La forma del perfil de la velocidad del sonido y este efecto de la curvatura de las ondas acústicas hacia las zonas donde esta velocidad es menor, es clave para la aparición de distintos tipos de propagación, tal y como se verá más adelante.

Pérdidas de transmisión
En la propagación de la señal acústica por el medio subacuático, ésta sufrirá distintas pérdidas debido a tres contribuciones principales: la divergencia geométrica, la absorción del medio y los rebotes producidos en las superficies. Estas pérdidas se engloban en un parámetro denominado pérdidas de transmisión, TL (transmission loss).
La divergencia geométrica se produce como consecuencia de la propagación de la onda acústica. La forma natural de propagación de una onda acústica es esférica, y por tanto la energía que transporta la señal se va repartiendo a medida que aumenta la distancia. Sin embargo, cuando la relación entre la distancia a la que se propaga la onda y la profundidad del fondo es tal que la onda queda confinada entre la superficie del mar y del fondo, se considera que la propagación es cilíndrica.
A priori, las pérdidas de transmisión se calculan a partir de la intensidad acústica, aunque es más cómodo utilizar una expresión en función de la distancia. Para una distancia determinada r, las pérdidas de transmisión por divergencia geométrica, si ésta es esférica, es el doble que si fuera cilíndrica. En concreto, para una divergencia esférica las pérdidas de transmisión, en dB, vienen dadas por (5), y para una divergencia cilíndrica, por (6) [1]:

Durante la propagación de la señal acústica, parte de la energía de ésta pasará al medio en forma de calor; este proceso se conoce como absorción por el medio, y consta de dos contribuciones principales: la viscosidad del agua y procesos de relajación. En agua dulce sólo aparece la primera de las contribuciones, mientras que la segunda aparece en agua salada, debido a los procesos de relajación iónica del sulfato de magnesio y del ácido bórico.
Estas contribuciones se recogen en el parámetro denominado coeficiente de absorción, que se expresa de forma semi-empírica, conociendo diversas fórmulas a lo largo de las últimas decadas. Una de las expresiones más utilizadas es la de Thorp (7), que data de finales de los años 60 y es válida hasta frecuencias de algunos kilohercios [17]:

Donde a tiene unidades de dB·km-1 y f es la frecuencia de la señal en kHz. El último término es una corrección que tiene en cuenta la absorción a muy baja frecuencia, siendo esta ecuación válida para temperaturas de 4ºC y una profundidad de 900 m, que es donde se tomaron las medidas [2].
Otra expresión más moderna, de principios de los años 80, es la suministrada por Francois y Garrison, válida para frecuencias entre 100 Hz y 1 MHz, y que se expresa según la ecuación (8) [18]:

Donde a tiene unidades de dB·km-1 y f es la frecuencia de la señal en kHz. El primer término proviene de la contribución del ácido bórico, el segundo de la contribución del sulfato de magnesio y el tercero de la viscosidad del agua, f1 y f2 son las frecuencias de relajación del ácido bórico y el sulfato de magnesio respectivamente, en kHz, y los coeficientes Ai y Pi pueden depender del pH, la salinidad, la profundidad, la temperatura y la velocidad del sonido.
Mediante la ecuación de Francois-Garrison se ha obtenido la gráfica que se muestra en la Figura 4, donde se representa la variación del coeficiente de absorción con la frecuencia, para el rango comprendido entre 100 Hz y 1 MHz. Este resultado se ha obtenido para un pH de 8, salinidad de 35‰, temperatura de 5ºC y una profundidad de 0 m.

Se puede obtener una conclusión importante a la vista de la Figura 4: para realizar transmisiones a distancias elevadas, del orden de varios kilómetros, habría que emplear frecuencias del orden de decenas de kHz, puesto que en caso contrario la absorción será demasiado grande; para transmisiones a distancias cortas, menores de 1 km, se podrían emplear frecuencias del orden de centenares de kHz.

La última contribución a las pérdidas de transmisión se debe a los rebotes de la señal en la superficie del mar o el fondo. En el caso de la superficie del mar, si ésta es totalmente lisa, la reflexión se puede considerar especular y apenas se pierde energía en el proceso. En el caso de que la superficie no sea lisa, parte de la señal se reflejará en direcciones distintas a la que tendría en el caso de una reflexión especular, por lo que se pierde energía. Se suele utilizar el parámetro de Rayleigh, dado en la ecuación (9), para caracterizar la regularidad de la superficie del mar [19]:
Donde k es el número de ondas, q  el ángulo de incidencia sobre la superficie del mar, y 2a es el valor rms de la altura de las olas, desde su punto más alto hasta el más bajo, considerando un tercio de las olas más altas. Mediante distintos experimentos, se ha podido determinar que para frecuencias inferiores al kHz las pérdidas de transmisión son de 1 dB/rebote, mientras que para frecuencias mayores que 25 kHz, estas pérdidas rondan los 3 dB/rebote [19]. Este aumento en las pérdidas se debe a que a medida que aumenta la frecuencia disminuye la longitud de onda, y por tanto afectarán al rebote irregularidades más pequeñas en la superficie, que en el caso de longitudes de onda mayores pasarían desapercibidas.
Para el caso del fondo marino, el estudio es a priori análogo, aunque resulta más complejo debido a la irregularidad que tiene el fondo en cuanto al terreno y material del que está compuesto. Existen diversos modelos que tratan de reproducir el comportamiento de los rebotes de la señal acústica en el fondo, desde el caso ideal del modelo de Rayleigh a otros como el de Sommerfeld o los geoacústicos. Además del rebote de la señal en el fondo, hay que tener en cuenta la capa de sedimentos sobre éste, que contribuye a la atenuación de la señal.
Teniendo en cuenta todas las contribuciones vistas, las pérdidas de transmisión se pueden expresar según la ecuación (10) para una propagación esférica, o la ecuación (11) para una propagación cilíndrica:
Donde la distancia r, que es donde se quieren medir las pérdidas (generalmente en el receptor), está expresada en metros, y se ha dejado de forma genérica la contribución de los rebotes, al depender de demasiadas condiciones y modelos para dar una expresión explícita.
[Referencias al final de la tercera parte]

Autor:

Joaquín Aparicio, Enrique García; Ana Jiménez; Fernando Álvarez†; Jesús Ureña
Departamento de Electrónica, Universidad de Alcalá
†Departamento de Ing. Eléctrica, Electrónica y Automática, Universidad de Extremadura

Más información o presupuesto