Modelos de transmisión
Existen diversos modelos matemáticos que estudian la propagación acústica en medios subacuáticos, destacando los modelos de trazado de rayos, modos normales, ecuación parabólica e integración espectral. Sin embargo, la configuración de estos modelos matemáticos requiere de diversos parámetros cuyo valor no siempre es conocido con exactitud, lo que puede conducir a resultados poco fiables.

Como consecuencia de este problema, han surgido a lo largo de las últimas décadas diversos modelos semi-empíricos para estudiar la propagación acústica en medios subacuáticos, distinguiendo distintos tipos de propagación. Como la inmensa mayoría de estudios se ha realizado sobre el mar, se hablará por defecto del medio marino, pero los resultados son aplicables a otros tipos de medios subacuáticos con las consideraciones oportunas.
No se va a profundizar en este artículo en los modelos matemáticos, aunque se comentará brevemente a continuación los resultados que proporciona el modelo de trazado de rayos, que es el más versátil y utilizado. El modelo de trazado de rayos se basa en la consideración de que la energía de la onda se puede concentrar en caminos definidos, de manera que se puede pensar en rayos en lugar de ondas. Esta consideración es válida siempre que la amplitud de la onda y la velocidad del sonido no varíen mucho en una longitud de onda, por lo que esta condición se cumplirá mejor para altas frecuencias, ya que la longitud de onda será más pequeña. El modelo de trazado de rayos calcula las ecuaciones que siguen los rayos, así como el campo de presiones que generan, a partir del cual se puede obtener las pérdidas de transmisión, y el tiempo de propagación de dichos rayos.

Propagación en aguas poco profundas
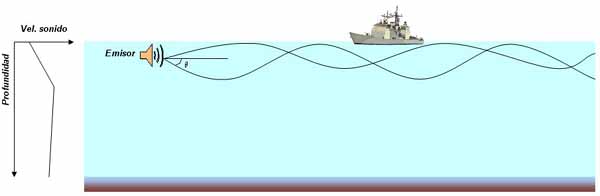
Cuando la profundidad a la que se encuentra el fondo es tal que se producen múltiples rebotes de la señal entre la superficie del mar y el fondo, se considera que la propagación se está realizando en un entorno de aguas poco profundas. La Figura 1 puede servir como ejemplo gráfico de este tipo de transmisión.
En la propagación en aguas poco profundas existe una interacción muy importante de la señal acústica con el fondo. Esta interacción es bastante compleja, puesto que hay que tener en cuenta el tipo de fondo, los sedimentos, cómo están distribuidos, las posibles variaciones que sufra en cuanto a su profundidad, etc. Todas estas dificultades hacen que el uso de modelos matemáticos como el de trazado de rayos sea arriesgado. Aparecen entonces los modelos semi-empíricos, entre los que destaca especialmente el modelo Colossus [20].
Este modelo se obtuvo a partir de una serie de medidas realizadas entre 100 Hz y  10 kHz. Tiene en cuenta la altura de las olas (en función del estado del mar), el tipo de fondo, la profundidad de la columna de agua, la frecuencia y el perfil de la velocidad del sonido. Este perfil se considera formado por dos segmentos constantes: desde la superficie del mar hasta una determinada profundidad L, en metros, la velocidad del sonido aumenta linealmente con la profundidad, mientras que para profundidades mayores que L, la velocidad disminuye con la profundidad hasta alcanzar el fondo.
Si se define la distancia de salto o de transmisión, H, como aquella distancia máxima a la que un rayo hace contacto con la superficie o con el fondo de la forma dada en la ecuación (12), donde D es la profundidad de la columna de agua en metros, se obtienen las pérdidas de transmisión según las ecuaciones dadas en (13) [20]:

 

  (12)

 

 

 

   (13)

 

Donde R es la distancia en km, a  el coeficiente de absorción en dB·km-1, kL es un parámetro denominado anomalía de campo cercano, que mide la ganancia debida a los rebotes entre el fondo y la superficie, en dB, y aT  es el denominado coeficiente de atenuación efectivo, que tiene en cuenta las pérdidas debidas al acoplamiento de energía entre la superficie y el fondo, expresado en dB/rebote. Los valores de estos dos últimos coeficientes aparecen tabulados para distintos tipos de fondo y estado del mar, por ejemplo en [2].

El canal superficial
En la región de la columna de agua cercana a la superficie es donde se obtienen las variaciones más importantes de temperatura. No obstante, el movimiento de masas de agua producido por las olas produce la mezcla del agua de esta región, de forma que se puede considerar isoterma. Si la salinidad es constante, la velocidad del sonido varía únicamente con la profundidad, obteniéndose entonces un gradiente positivo de la velocidad del sonido con la profundidad hasta cierta profundidad, donde aparece la termoclina.
Como las ondas acústicas se curvan hacia las zonas de menor velocidad del sonido, si se coloca un emisor en esta región cercana a la superficie, que se denomina canal superficial, las ondas acústicas queden atrapadas dentro de éste si el ángulo de emisión es suficientemente pequeño y la longitud de onda no es mayor que la anchura del canal. De este modo, la señal acústica se propaga rebotando con la superficie del mar y curvándose para volver a rebotar contra esta superficie, sin tocar el fondo, tal y como muestra la Figura 5.
Hay que tener en cuenta que la señal se propaga de forma esférica al principio, pero a partir de cierta distancia rt, denominada distancia de transición, se puede considerar la propagación como cilíndrica, al estar confinada la energía. En este caso, las pérdidas de transmisión se pueden expresar según la ecuación (14), donde la distancia de transición viene dada por la ecuación (15) [2]:

 

   (14)

 

   (15)

 

Donde r es la distancia en metros, a  es el coeficiente de absorción en dB·km-1 y aL es el denominado coeficiente de fugas, también en dB·km-1. Este coeficiente de fugas tiene en cuenta la energía que escapa del canal debido al scattering de la señal en la superficie y a la difusión transversal, que se origina en la discontinuidad del perfil de la velocidad del sonido en la base del canal; H es la profundidad del canal en metros, y q el ángulo del rayo atrapado con mayor inclinación dentro del canal, tal y como muestra la Figura 5.

El canal acústico profundo
En la Figura 3 se representaba un perfil típico para latitudes medias. En este perfil, a la profundidad de 1 km aproximadamente, aparecía un mínimo en la velocidad del sonido. Este mínimo marca el denominado eje del canal acústico, y provocará que una señal acústica emitida en las cercanías de esta profundidad se curve hacia este mínimo, por lo que si el ángulo de emisión es lo suficientemente pequeño, la señal se propaga sin rebotar con la superficie o el fondo. Se forma así un canal de propagación, denominado canal acústico profundo, representado en la Figura 6.
En este caso, las pérdidas de transmisión vendrán dadas por la divergencia geométrica de la señal y la absorción del agua. En un principio la divergencia geométrica será esférica, hasta que alcanza la distancia de transición rt, a partir de la cual se puede considerar que es cilíndrica. No existe ahora contribución debido a los rebotes en el fondo o en la superficie del mar. Las pérdidas de transmisión se pueden expresar según la forma dada en (16), siempre y cuando la distancia r sea tal que la divergencia ya sea cilíndrica [1]:

   (16)

 

Donde r es la distancia en metros donde se quieren calcular las pérdidas de transmisión, y a es el coeficiente de absorción en dB·km-1. La distancia de transición se puede calcular según la ecuación (17) [1]:

 

   (17)

 

 

Donde Ds es la profundidad a la que se sitúa el mínimo de la velocidad del sonido en el canal superficial, zs es la profundidad del emisor medida desde la base del canal superficial, que marca el inicio del canal acústico profundo, y rs es la distancia de salto. Esta distancia de salto depende de las distancias entre el eje acústico y los límites del canal acústico profundo, del valor de la velocidad del sonido en la base del canal superficial, y de la diferencia entre este valor y el mínimo, obtenido en el eje del canal acústico.

Otras formas de propagación y comentarios adicionales
Se han comentado hasta ahora los tres canales más relevantes en una propagación acústica en cuanto a la importancia de la forma del perfil de la velocidad del sonido, pero existen otras formas de propagación. Además del camino directo, es decir, una transmisión directa entre emisor y receptor, que se dará para distancias muy cortas, hay que destacar las zonas de convergencia, el canal acústico confiable y los canales árticos.

Las zonas de convergencia se forman por la acumulación de rayos en una determinada zona cercana a la superficie, pero sin tocar el fondo o la propia superficie del mar, lo que provoca un reforzamiento de la señal. En estas zonas las pérdidas de transmisión serán menores debido a la aparición de un término denominado ganancia de convergencia.
El canal acústico confiable aparece cuando se tiene un emisor a una profundidad elevada, por debajo del eje acústico, y un receptor cercano a la superficie. Al emitir la señal, la capa isotérmica profunda hará que los rayos se curven hacia la superficie, donde llegarán al emisor sin tocar ni el fondo ni la superficie, y como no interacciona con ninguna de ellas, se denomina confiable.
En los canales árticos puede existir una capa de hielo sobre la superficie del mar, lo que aporta una fuente de ruido extra por la ruptura y caída de trozos de hielo al agua, y más incertidumbre en la reflexión de los rayos debido a la irregularidad de esta capa de hielo, además de procesos de scattering. Las condiciones de temperatura de estas regiones forman un perfil de la velocidad del sonido en donde dicha velocidad aumenta linealmente con la profundidad de forma permanente, por lo que se puede considerar que el eje acústico se sitúa en la superficie. Todos los rayos emitidos acabarán curvándose hacia la superficie y rebotando contra ésta e interaccionando con la capa de hielo, que actúa como un filtro paso-bajo debido al scattering.
En general, los modelos estudiados pueden dar una buena aproximación de los valores de las pérdidas de transmisión que se obtendrían para un caso determinado. Sin embargo, existen factores adicionales que pueden influir en el resultado y que no están presentes, como turbulencias, remolinos, corrientes internas o ruido ambiental. Todos estos factores pueden alterar los resultados obtenidos, tal y como se verá en la segunda parte de este trabajo.

[Referencias al final de la tercera parte]

Autor:

Joaquín Aparicio, Enrique García; Ana Jiménez; Fernando Álvarez†; Jesús Ureña
Departamento de Electrónica, Universidad de Alcalá
†Departamento de Ing. Eléctrica, Electrónica y Automática, Universidad de Extremadura

Más información o presupuesto