Mecanismos adicionales en la propagación acústica subacuática
En la propagación acústica subacuática, como se ha analizado anteriormente, influyen de manera especial la forma del perfil de la velocidad del sonido, y el valor de la atenuación que sufra la señal, debido a la divergencia geométrica y los procesos de absorción y rebotes.

Sin embargo, considerar únicamente estos efectos conformaría un caso ideal dentro de las aplicaciones prácticas. Numerosos mecanismos adicionales pueden aparecer cuando se realiza una propagación acústica en medios subacuáticos, algunos de los cuales provocarán fluctuaciones de la señal, tanto en amplitud como en fase. Por defecto, se hablará de medios marinos, pero en general estos efectos pueden aparecer en otros medios subacuáticos.

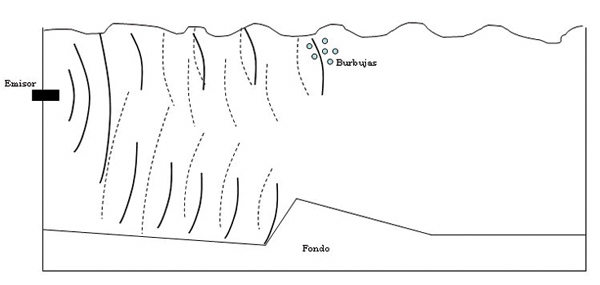
Un mecanismo que aparecerá siempre será la reverberación. La reverberación es la energía dispersada en otras direcciones como resultado de la interacción de las ondas acústicas con el medio, como los rebotes en las superficies o el encuentro de las ondas con partículas en suspensión en el agua. La Figura 7 muestra un ejemplo de distintos procesos de reverberación, donde en trazo discontinuo aparece la señal reflejada que provoca reverberación.

Se pueden considerar dos tipos de reverberación: volumétrica y superficial. La reverberación volumétrica se produce en el volumen de agua donde tiene lugar la propagación, y se debe fundamentalmente a las partículas en suspensión y a la existencia de vida marina. Hay que destacar especialmente la contribución a la reverberación volumétrica de la capa de scattering profunda, de origen biológico, y que proporciona un nivel de scattering superior al resto [2]. Debido a este origen biológico, la capa de scattering profunda tiene un comportamiento variable en lo que respecta a su profundidad a lo largo del día, en función del movimiento de los animales, y a la respuesta que proporciona a diferentes frecuencias de la señal acústica, en función del tamaño de estos, lo que muestra que está formada por diversas subcapas.

La reverberación superficial procede del scattering producido por la interacción de las ondas acústicas con las superficies y partículas próximas a ellas, como sedimentos o capas de burbujas introducidas por las olas o el paso de los barcos, por ejemplo. En lo que respecta a la superficie del mar, el nivel de scattering dependerá de la frecuencia, el ángulo de incidencia y la irregularidad de dicha superficie, donde esta irregularidad dependerá de la velocidad del viento en la superficie [2]. Si existe además una capa de hielo sobre esta superficie, la reverberación producida será mayor. En el fondo, el nivel de scattering dependerá además del material del que está formado: fondos rocosos provocan más reverberación que fondos arenosos. La contribución del fondo a la reverberación es la más compleja de predecir, puesto que la interacción de las ondas acústicas con el fondo es la más complicada de resolver.

Por otra parte, las burbujas de gas presentes en el agua acaban formando parte de los procesos de compresión y rarefacción de la onda, donde la magnitud de esta respuesta a la señal acústica dependerá de la frecuencia y del tamaño de las burbujas. En este proceso, las ondas acústicas pierden energía en favor de las burbujas, que las radiarán en todas direcciones, provocando la reverberación, que será máxima cuando las burbujas entran en resonancia [2].

Además de este efecto, y aunque no es reverberación, cabe mencionar que las burbujas de gas provocan la variación de la velocidad del sonido al pasar por una región donde esté presente una capa de burbujas. Si el tamaño de las burbujas es menor que el de resonancia para la frecuencia de la señal, la burbuja se comprime durante la fase de compresión de la onda acústica, se reduce entonces el módulo de compresibilidad y se reduce por tanto la velocidad del sonido; si el tamaño es mayor, la burbuja se expande durante la fase de compresión, aumenta el módulo de compresibilidad y aumenta por tanto la velocidad del sonido [3]. Estas variaciones de la velocidad del sonido afectarán a la forma del perfil, con las consecuencias que esto conlleva.

De forma general, si se emite un pulso sinusoidal la señal procedente de la reverberación aparecerá como un tono irregular que va decayendo con el tiempo, aunque pueden aparecer picos de intensidad en algunos instantes. Este tono sufrirá un desplazamiento en frecuencia y un ensanchamiento del espectro, debido al movimiento de las partículas en suspensión, fauna marina, la posibilidad de que la reverberación recibida de diferentes direcciones haya sufrido desplazamientos Doppler diferentes, etc. La reverberación será mayor a medida que aumenta la potencia transmitida y la señal acústica se emita en un rango de ángulos más amplio.

El efecto Doppler es otro de los mecanismos adicionales a considerar. Dada la naturaleza del medio subacuático, el emisor o el receptor (o ambos) pueden estar en movimiento al realizar las medidas, como por ejemplo, en un barco (Figura 8). En ese caso, se produce el efecto Doppler, consistente en un desplazamiento de la frecuencia; si la señal puede recorrer distintos caminos (multicamino), aparecen diferentes desplazamientos Doppler que dan lugar a un ensanchamiento del espectro en el receptor.

Además, aunque los instrumentos estuvieran perfectamente quietos, puede existir también un ensanchamiento Doppler debido al movimiento de masas de agua mientras se transmite la señal, como el que se da en las olas, que alteran la superficie de reflexión. Otra contribución puede venir por las corrientes internas, provocando el desplazamiento de masas de agua, lo que afectará a la propagación acústica.
Para evitar las consecuencias de este ensanchamiento, la duración de la señal debe cumplir la relación dada en la expresión (18) [7]:

1        
__  >> B    (18)
T

Donde T es la duración de la señal y B el ensanchamiento Doppler. Este ensanchamiento Doppler aumenta con la frecuencia, por lo que será de especial importancia en distancias cortas (un kilómetro o menores), donde se pueden emplear varias decenas de kHz [4].
El ensanchamiento Doppler resulta de interés junto al retardo asociado al multicamino, que aparecerá debido a los rebotes en la superficie y a la refracción de los rayos hacia el mínimo de la velocidad del sonido, por lo que la disposición del emisor y el receptor es crítica. El retardo de multicamino es el tiempo entre la llegada de la primera señal y la del camino más largo.

Una propagación en el eje de distancias puede provocar un ensanchamiento temporal debido al multicamino bastante importante, provocando el efecto conocido como interferencia entre símbolos, ISI (de Intersymbol Interference). Como ejemplo, para una tasa de transmisión de 10 ksps (kilosímbolos por segundo) sobre un canal de aguas poco profundas que se puede extender entre 1 y 10 km, se produce un retardo de multicamino de 10 ms, que provocará que la ISI se extienda sobre 100 símbolos [4]. Para evitar los efectos de estas múltiples llegadas al receptor procedentes del multicamino, se debe cumplir la relación dada en la ecuación (19) [7]:

1        
__  >> tL   (19)
W

Donde W es el ancho de banda y tL el retardo de multicamino. Lo que se busca en todos los sistemas es que el producto B·tL sea menor que la unidad; en caso contrario se dice que el sistema está sobre-ensanchado y no se puede usar el canal de forma correcta salvo que se trate previamente la señal acústica.
Además de estos efectos, hay que tener en cuenta que el medio subacuático es dinámico, es decir, existen diversos procesos que provocan cambios en el medio. Estos procesos se suelen clasificar en función de la extensión espacial que presentan, en fenómenos de gran escala (más de 100 km), de mesoescala (entre 100 m y 100 km) y de pequeña escala (menos de 100 m) [19].

Entre los fenómenos de gran escala se encuentran la circulación debida al viento producida en los primeros cientos de metros de profundidad, y la circulación termohalina, debida a cambios en la densidad producidos por variaciones en la temperatura y salinidad del agua.
Dentro de los fenómenos de mesoescala se encuentran los frentes oceánicos, los remolinos y las ondas internas. Los frentes oceánicos son zonas de transición que separan masas de agua de características diferentes, especialmente temperatura y salinidad. Los remolinos consisten en masas de agua que fluyen de forma circular cerrándose sobre sí mismas, por lo que se pueden considerar un caso particular de frente oceánico, al mostrar unas características distintas que sus alrededores. Por su parte, las ondas internas son ondas que se propagan por las interfases entre capas de fluidos de distinta densidad, o en un mismo fluido que presente un gradiente de densidad.
Por último, entre los fenómenos de pequeña escala destaca el conocido como escalera termohalina, que aparece generalmente en la termoclina principal y que consiste en zonas de varios metros de profundidad donde la temperatura y la salinidad son uniformes, separadas por otras donde existe un gradiente apreciable en estas magnitudes. Este efecto aparece más frecuentemente en zonas donde existe mezcla de agua dulce con salada.

Otro mecanismo a tener en cuenta es la dispersión de la velocidad del sonido (a distinguir del scattering). La dispersión consiste en la propagación a distinta velocidad de las componentes de diferente frecuencia de la señal. Debido a que generalmente no está presente, las fórmulas semi-empíricas que aparecen en la bibliografía no tienen en cuenta esta dependencia; sin embargo, puede aparecer bajo determinadas circunstancias, como por ejemplo atravesar una capa de burbujas [21] o según la forma que tenga el canal (dispersión geométrica) [22]. Los efectos de dispersión pueden ser muy importantes si se codifica la señal acústica, puesto que esta señal puede llegar irreconocible al receptor.

El último mecanismo a considerar es el ruido ambiental, es decir, toda aquella señal que se sigue recibiendo cuando se ha eliminado toda fuente de ruido conocida. Este ruido ambiental se suele escuchar como un murmullo de baja frecuencia, generalmente del orden del hercio.
En alta mar, cuando se puede considerar una propagación de aguas profundas, existen diversas fuentes posibles de ruido ambiental: las olas, mareas y turbulencias, que provocan cambios en la presión que registran los hidrófonos, la ruptura de las olas en la superficie del mar y la de las burbujas en el agua, movimientos sísmicos, la presencia de barcos y el denominado ruido térmico de las moléculas. Casi todas estas contribuciones son de baja frecuencia, generalmente inferiores a 100-500 Hz, excepto la ruptura de olas y burbujas, que pueden llegar a 30 kHz, y el ruido térmico, que puede llegar a los 100 kHz [2].

En aguas poco profundas, las fuentes posibles de ruido ambiental son conocidas también, pero su variabilidad, tanto espacial como temporal, es mayor. Estas fuentes son la pesca y el ruido provocado por la industria, el viento y el ruido biológico, provocado por la vida animal, como por ejemplo los crustáceos. De forma general, el ruido ambiental en aguas poco profundas afecta más a bajas frecuencias, al igual que en el caso anterior.

Existen dos contribuciones más. Una es común a las aguas profundas y poco profundas, y consiste en el ruido provocado por las gotas de lluvia al chocar contra la superficie del mar. Este ruido puede llegar a frecuencias de 10 kHz [2]. La otra contribución es específica de regiones polares, donde la pesca y el viento afectan en menor medida debido a la capa de hielo que cubre la superficie del mar, pero la ruptura de estas capas es una fuente de ruido importante y que puede llegar hasta frecuencias de 1 kHz [19].

Simulaciones
Se muestran a continuación diversas simulaciones realizadas por el método de trazado de rayos, que es el más utilizado en la bibliografía. Se distinguen tres casos fundamentales: canal de aguas poco profundas, el canal superficial y el canal acústico profundo. En todos los casos, se considera una columna de agua, de densidad      1024 kg·m-3, sobre un fondo de arena fina, de densidad 1941 kg·m-3. No se considera la presencia de ondas transversales en el fondo, que por otra parte es totalmente liso, al igual que la superficie del mar. En todos los cálculos de las pérdidas de transmisión se ha considerado la fase de los distintos rayos (cálculo coherente), puesto que se han asumido superficies totalmente lisas, y no existe por tanto incertidumbre en la interacción de la señal con estas superficies.

Simulación de un entorno de aguas poco profundas
Se muestra en primer lugar la propagación acústica en un entorno de aguas poco profundas, es decir, caracterizado por varios rebotes entre el fondo y la superficie. En este caso particular, el fondo está situado a 100 m de profundidad, y se supone una red de receptores, situados cada 5 m de profundidad, a 2 km de distancia del emisor, que se encuentra a 10 m de profundidad.
El perfil de la velocidad del sonido viene dado por la Figura 9, que muestra una velocidad constante en el agua igual a 1500 ms-1, y una velocidad constante en la arena fina igual a 1749 ms-1.

Los rayos se emiten con unos ángulos comprendidos entre ±10º, a una frecuencia de 30 kHz. La Figura 10 muestra el camino que siguen dichos rayos hasta el receptor, donde se ha elegido representar 21 rayos por motivos de claridad visual. En esta figura se puede observar cómo hay rayos que llegan sin rebotar hasta la red de receptores, mientras que otros sufren algún rebote con el fondo o la superficie, o varios rebotes con ambas.

La Figura 11 muestra las pérdidas de transmisión en función de la distancia y la profundidad. Para calcular estas pérdidas, se ha dejado que el algoritmo elija el número de rayos que estime oportuno (muy superior a 21 rayos). Se puede apreciar en esta figura cómo hay zonas donde la señal interfiere de forma destructiva, en función de cómo sean las fases de las señales que convergen en esa zona, obteniendo zonas donde las pérdidas de transmisión decaen considerablemente a distancias cercanas al emisor.
En la Figura 12 aparece representada la variación de las pérdidas de transmisión y la fase respecto a la profundidad, para la distancia de 2 km, donde estarían los receptores. Los valores obtenidos para las pérdidas de transmisión coinciden con lo esperado para una divergencia geométrica a 2 km de distancia y la contribución de la absorción, que para la frecuencia de 30 kHz viene a ser aproximadamente de 8 dB·km-1. La fase sufre también varias fluctuaciones debido a la interacción con la superficie del mar y a la interferencia entre distintos rayos.
La Figura 13 representa las distintas llegadas de rayos a los receptores, es decir, el multicamino. Por ejemplo, para el receptor situado a 5 m, se detecta un primer rayo para un tiempo de propagación de aproximadamente 1.334 s (tiempo coherente con la distancia y la velocidad del sonido considerada), luego detecta cinco rayos muy seguidos alrededor de 1.34 s, y por último detecta otro rayo para un tiempo de propagación de 1.357 s, aproximadamente.

Simulación del canal superficial
Se presenta ahora la simulación de la propagación acústica en un canal superficial. El perfil de la velocidad del sonido se muestra en la Figura 14, donde la velocidad en la superficie es de 1485 ms-1 y va aumentando hasta alcanzar los 100 m de profundidad. A partir de ese punto, su valor es constante e igual a 1500 ms-1. La red de receptores se sitúa a 2 km de distancia del emisor, que está a 50 m de profundidad, suponiendo un receptor cada 5 m. La frecuencia de emisión es de 20 kHz, donde los rayos salen con ángulos comprendidos entre ±10º, y la profundidad a la que está el fondo es de 500 m.

En la Figura 15 se representan los caminos seguidos por los rayos en este canal,  donde al igual que en el caso anterior, se han elegido 21 rayos por el mismo motivo. En esta figura se puede apreciar la curvatura que sufren los rayos hacia la superficie, donde se está el mínimo de la velocidad del sonido. En este caso no existe interacción con el fondo para la distancia a la que se sitúan los receptores, únicamente hay rebotes con la superficie del mar.
Las pérdidas de transmisión en función de la distancia y la profundidad se representan en la Figura 16. En esta figura se observa, al igual que en el caso de aguas poco profundas, un patrón de interferencias formado por la interacción de rayos con distintas fases. Aparece ahora una zona situada a la distancia de los receptores y a unos 50 m de profundidad, donde las pérdidas son considerablemente menores que en su entorno; esto se debe a la concentración de rayos en esta zona, tal y como también se puede apreciar en la Figura 15.
En la Figura 17, donde aparece la variación de las pérdidas de transmisión y la fase con la profundidad en los receptores, aparece también este mínimo en las pérdidas de transmisión, donde se aprecia la clara diferencia en los valores de las pérdidas para esta profundidad. La Figura 18 representa el multicamino obtenido para este caso que, de forma general, presenta menos detecciones para cada receptor que en aguas poco profundas, excepto el receptor situado a 50 m de profundidad. Esto se debe a que existen menos rebotes entre las superficies, y por tanto el multicamino será menor.

Simulación del canal acústico profundo
La última de las simulaciones presentadas es la del canal acústico profundo. La Figura 19 muestra el perfil que se ha considerado para este caso, donde la velocidad tiene un valor constante de 1510 ms-1 desde la superficie hasta los primeros 100 m, para posteriormente descender hasta 1485 ms-1 en el eje acústico, situado a 1 km; aumenta a continuación linealmente hasta alcanzar de nuevo los 1510 ms-1 en el fondo, a 4 km de profundidad. Los receptores se sitúan a 50 km de distancia, suponiendo uno cada 5 m, al igual que en los casos anteriores; el emisor está en el eje acústico. En este caso se ha empleado una frecuencia de 500 Hz para simular en todo lo posible un caso práctico, puesto que a 30 kHz las pérdidas en los receptores rondarían los 500 dB debido fundamentalmente a la absorción, por lo que sería una frecuencia inviable en la realidad para transmitir a esta distancia. Los rayos se emiten entre ±10º.

La Figura 20 muestra las pérdidas de transmisión obtenidas para la distancia y la profundidad, donde se puede apreciar que las pérdidas de transmisión en la región cercana al eje acústico son menores que en las demás, debido al efecto de refracción de los rayos hacia esta zona, provocando la acumulación de estos. Por su parte, la Figura 21 representa la variación de las pérdidas y la fase respecto a la profundidad, en los receptores. En esta gráfica también se puede observar el mínimo en las pérdidas que se obtiene para la profundidad del eje acústico.

Conclusiones
En este artículo se ha presentado una revisión de los fundamentos de la propagación acústica en medios subacuáticos, remarcando la importancia del conocimiento del perfil de la velocidad del sonido para la posterior propagación de una señal por diversos canales. Se han visto las ecuaciones teóricas más importantes para la velocidad del sonido, la absorción y las pérdidas para los distintos canales, y se han presentado de forma cualitativa diversos efectos que pueden afectar a la propagación acústica subacuática. Adicionalmente, se han mostrado diversas simulaciones realizadas para los tres canales más significativos.

Agradecimientos
Este trabajo ha sido posible gracias al soporte de la empresa GCM Communications Technology. Para las simulaciones realizadas se ha empleado la herramienta Acoustic Toolbox, para Matlab, disponible en la página web del Centre for Marine Science and Technology (Curtin University of Technology, Australia) [23].

Autores:

Joaquín Aparicio, Enrique García; Ana Jiménez; Fernando Álvarez†; Jesús Ureña
Departamento de Electrónica, Universidad de Alcalá
†Departamento de Ing. Eléctrica, Electrónica y Automática, Universidad de Extremadura

Bibliografía
[1]    Lawrence E. Kinsler, Austin R. Frey, Alan B. Coppens y James V. Sanders,
“Fundamentals of Acoustics”, Ed. John Wiley & Sons, 4ª Edición, 2000.
[2]    Robert J. Urick, “Principles of Underwater Sound”, Ed. Península Publishing,
3ª Edición, 1983.
[3]    T.G. Leighton, capítulo “Fundamentals of Underwater Acoustics”, pp. 373-443,
en Fundamentals of Noise and Vibrations, Frank Fahy y John Walker, Ed.
Taylor and Francis, 1ª Edición, 1998.
[4]    Milica Stojanovic, “Acoustic (Underwater) Communications”, en Wiley
Encyclopedia of Telecommunications, John G. Proakis, Ed. John Wiley &
Sons, 1ª Edición, 2003.
[5]    Chauncey S. Miller y Carl E. Bohman, “An Experiment in High Rate Underwater
Telemetry”, en OCEAN 84, Vol. 4, pp. 34-48, 1972.
[6]    Azizul H. Quazi y William L. Konrad, “Underwater Acoustic Communication”, en
IEEE Communications Magazine, Vol. 20, No. 2, pp. 24-30, 1982.
[7]    Arthur B. Baggeroer, “Acoustic Telemetry – An Overview”, en IEEE Journal of
Oceanic Engineering, Vol. 9, No. 4, pp. 229-235, 1984.
[8]    M. Suzuki, T. Sasaki y T. Tsuchiya, “Digital Acoustic Image Transmission
System for Deep-Sea Research Submersible”, en OCEANS’92 Proceedings,
Vol. 2, pp. 567-570, 1992.
[9]    R. Galvin y R.F.W. Coates, “Analysis of the Performance of an Underwater
Acoustic Communications System and Comparison with a Stochastic Model”,
en OCEANS’94 Proceedings, Vol. 3, pp. 478-482, 1994.
[10]    Milica Stojanovic, “Recent Advances in High-Speed Underwater Acoustic
Communications”, en IEEE Journal of Oceanic Engineering, Vol. 21, No. 2,
pp. 125-136, 1996.
[11]    E.M. Sozer, J.G. Proakis, M. Stojanovic, J.A. Rice, A. Benson y M. Hatch,
“Direct Sequence Spread Spectrum Based Modem for Underwater Acoustic
Communication and Channel Measurements”, en Proceedings of MTS/IEEE
OCEANS’99, pp. 228-233, 1999.
[12]    Daniel Kilfoyle, “Spatial Modulation in the Underwater Acoustic Channel”.
Editado por Ft. Belvoir Defense Technical Information Center. Página gestio-
nada por Massachusetts Institute of Technology, disponible en:
http://www.ll.mit.edu/asap/asap_04/DAY2/36_PA_KILFOYLE.PDF
[13]    Ian F. Akyildiz, Dario Pompili y Tommaso Melodia, “Underwater Acoustic
Sensor Networks: Research Challenges”, en Ad Hoc Networks, Vol. 3, No. 3,
pp. 257-279, 2005.
[14]    Milica Stojanovic, “OFDM for Underwater Acoustic Communications: Adaptive
Synchronization and Sparse Channel Estimation”, en IEEE International
Conference on Acoustics, Speech and Signal Processing (ICASSP) 2008,
pp. 5288-5291, 2008.
[15]    Subhadeep Roy, Tolga M. Duman, Vincent McDonald y John G. Proakis, “High-
Rate Communication for Underwater Acoustic Channels Using Multiple
Transmitters and Space-Time Coding: Receiver Structures and Experimental
Results”, en IEEE Journal of Oceanic Engineering, Vol. 32, No. 3, pp. 663-
688, 2007.
[16]    “Technical Guides: Speed of Sound in Sea-Water”, página gestionada por
Communication Technology. Disponible en:     
http://www.comm-tec.com/Library/Technical_Papers/speedsw.pdf
[17]    Milica Stojanovic, “On the Relationship Between Capacity and Distance in an
Underwater Acoustic Communication Channel”, en Proc. First ACM
International Workshop on Underwater Networks (WUWNeT’06) / MobiCom
2006. Disponible en:
http://www.mit.edu/~millitsa/resources/pdfs/wuw37-stojanovic.pdf
[18]    Mari Carmen Domingo, “Overview of Channel Models for Underwater Wireless
Communication Networks”, en Physical Communication, Vol. 1, No. 3,
pp. 163-182, 2008.
[19]    Paul C. Etter, “Underwater Acoustic Modeling and Simulation”, Ed. Taylor and
Francis, 3ª Edición, 2003.
[20]    M. Schulkin y J.A. Mercer, “Colossus Revisited: A Review and Extension of the     
Marsh-Schulkin Shallow Water Transmission Loss Model”, Applied
Physics Laboratory, University of Washington, APL-UW 8508, 1985.
[21]    Herman Medwin y Clarence S. Clay, “Fundamentals of Acoustical
Oceanography”, Ed. Academic Press, 1ª Edición, 1998.
[22]    I.B. Esipov, O.E. Popov, V.A. Voronin y S.P. Tarasov, “Dispersion of the Signal
of a Parametric Array in Shallow Water”, en Acoustical Physics, Vol. 55, No.
1, pp. 76-80, 2009.
[23]    Centre for Marine Science and Technology, página gestionada por Curtin
University of Technology, disponible en: http://cmst.curtin.edu.au.

Más información o presupuesto